2017-2018

Archived Mathletes Problems of the Week   

 Solutions

MPOW #1: Maximaze / Minimaze

a) The lowest possible score is 18.

b) The highest possible score is 2,824.

a) P = 4

b) S = 7 

a) There are 4 possible paths that will allow the knight to land on each square exactly once and return back to its starting square. Here is one:

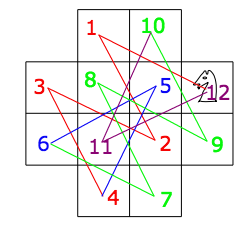
b) The knight can always find such a path through this board, no matter what square it starts on. In fact, there are 4 possible paths for each starting square.

a) There are 19 different selections that will result in an even sum.

b) Surprisingly, when we choose three numbers instead of four, there are still exactly 19 different selections that will result in an even sum.

a) To find Harry, you should open door 2.

b) To find Harry, you should open door 2.

c) To find Harry, you should open door 1.

a) Old MacDonald has 216 animals on his farm.

b) Old MacDonald has 16 grown cats and 4 kittens in his house.

Here is one possible solution. There are many others.

a) If you label the figures with letters from top row to bottom row, left to right, the following figures have an Euler trail: a, b, c, g, h, j

b) Figures where all the points have an even number of lines coming out of them will have Euler Trails (as in b, c, g, and h). If there are exactly two points with an odd number of lines coming out of them, there will also be an Euler trail (as in a and j). If a figure has one, three or more points with an odd number of lines, there is no Euler trail (as in d, e, f, and i). 

a) The building is 40 feet tall.

b) Jamal started with 7 Pokemon cards.

c) This problem is a paradox posed by British philosopher, James Thompson, and is a version of the classic dichotomy paradox by Zeno. Although the lamp must be either on or off at the end of two minutes, it is impossible to determine which state it will be in. This is because the fractional lengths of time (1, 1/2, 1/4, 1/8, 1/6, 1/32...) continue infinitely, never actually reaching 2 minutes. There is no final number before 2 minutes, so we cannot determine which way the switch will move at precisely 2 minutes. 

The substitution key is:

The secret message was: 

Big news! Brookline School District says an extra-curricular "zombie survival class" at Pierce School is no more. It has been replaced by a "calming meditation class." Principal Lesley Ryan-Miller says she was unaware of the zombie class until she read an article about its popularity in the Penguin Post. Miller says she "couldn't believe that would actually be a class." Some parents had questioned the educational value of the class. Others wanted to take it themselves.

a) The 2,018th term is 5.

b) There will be 400 purple squares in the 99th figure.

c) The sum is equal to 99/100.

a) The two solutions are: "thirty-six" and "thirty-eight".

b) To make the sentence true, there should be "seven" s's, "four" i's, and "five" e's.