2018-2019

Archived Mathletes Problems of the Week   

 Solutions

MPOW#1: As Easy as 1, 2, 3

a) 1,332

b) 66,660

c) If n is the number of digits, the sum will be: (n-1)! * (n/2 * (n+1)) * (1 + 10 + 100 + 1000 +... + nth place value)

a) The first entry would be 8 (eight). 

b) The last entry would be 202 (two hundred two).

c) The first odd entry would be 885 (eight hundred eighty-five).

d) The last odd entry would be 223 (two hundred twenty-three).

e) The first entry would still be 8 (eight) but the last entry would now be 2,000,000,002,202 (two trillion two thousand two hundred two).

a) Starting with the numbers 1, 2, 3, 4, the final number will be even.

b) Starting with the numbers 1, 2, 3, 4, 5, the final number will be odd.

c) There is a pattern, which can be described in a few different ways. One way to predict the outcome is to find the sum of the starting numbers. If it is even, the final number will be even; if it is odd, the final number will be odd.

a) With three people, three conversations are necessary.

b) With four people, five conversations are necessary.

c) With five people, seven conversations are necessary. With six people, nine conversations are necessary.

d) A mathematical rule for finding the fewest number of conversations needed for any number of people (greater than one) is 2n - 3.

There are several possible solutions for each network. One solution for each is shown below.

a) 

b)

c) 

Quiz #1

1. A

2. A

3. C

Quiz #2

1. B

2. C

3. A

4. B

a) Some other amounts you cannot buy exactly include 1¢, 2¢, 4¢, 5¢, 7¢, 8¢...

b) The largest amount you cannot buy exactly is 47¢.

c) In total, there are 24 amounts of postage you cannot buy exactly.

d) If there were only 4¢ and 100¢ stamps available, there would be an infinite number of postal amounts you could not buy exactly. This is because you will only be able to purchase amounts that are multiples of 4¢.

a) One solution is: Blip, Bleep, Bloop, Bleep, Blip, Bleep.

b) You need at least 6 commands to put the aliens in reverse order. There are 16 ways to do this.

c) With the Glip, Gleep, and Gloop commands you still need at least 6 commands. One possible solution is: Glip, Gleep, Gloop, Glip, Gleep, Gloop.

a)

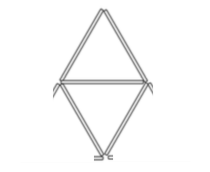
b)

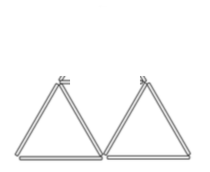
c)

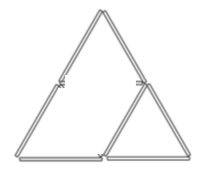
d)

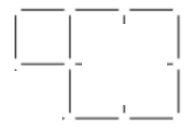
e)

a) No, 5 is the fewest number of consecutive integers that will sum to 100: add 18 through 22.

b) The largest number of consecutive integers that will sum to 100 is 200: add the numbers -99 through 100.

c) The fewest number of consecutive integers that will sum to 1000 is also 5: add 198 through 202.

d) The largest number of consecutive integers that will sum to 1000 is 2000: add the numbers -999 through 1000.

a) With 3 cuts, the maximum number of pieces you can get is 7.

b) with 4 cuts, the maximum number of pieces you can get is 11.

c) There is a pattern. One way to describe this pattern is with the following recursive formula where P represents the number of pieces and C represents the number of cuts.  

P_c = P_c-1 + c

We can also find an explicit formula that will allow us to calculate the maximum number of pieces for a certain number of cuts even if we don't know how many pieces there were before: 

½ (c² + c + 2)

a) There are several possible solutions. Here are three:

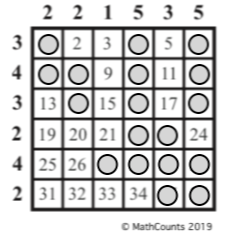
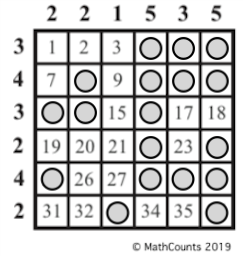
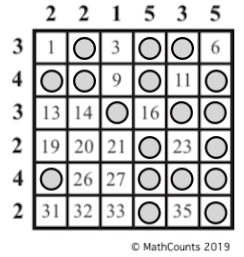
b) The sum of the numbers on which Hiroshi placed coins is 326.

c) There are many possible ways to place the coins, but the sum of the numbers covered will always be 326. In fact, we do not need to find an arrangement of the coins at all to show that the sum will always be 326. By describing each square in the solution as a multiple of 6 (its row minus 1) plus a specific number (its column), we can use the information given to us to describe the solution as follows: 

(0 x 6 ) + (0 x 6) + (0 x 6) + (1 x 6) + (1 x 6) + ( 1 x 6) + (1 x 6) + (2 x 6) + (2 x 6) + (2 x 6) + (3 x 6) + (3 x 6) + (4 x 6) + (4 x 6) + (4 x 6) + (4 x 6) + (5x 6) + (5 x 6) + 1 + 1 + 2 + 2 + 3 + 4 + 4 + 4 + 4 + 4 + 5 + 5 + 5 + 6 + 6 + 6 + 6 + 6

This sum describes every possible solution and is equal to 326.

a) The 20th Fibonacci number is 6,765.

b) Here are some of the numbers that precede the first 1 (the original sequence is in bold): ....34, -21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8.... Notice that the numbers that precede the first one reproduce the original Fibonacci sequence but every other tern is negative.

c) The missing numbers are 101, 605, 706, 1311.

a) 

a) Here is one possible factor graph for the numbers 2 - 10.

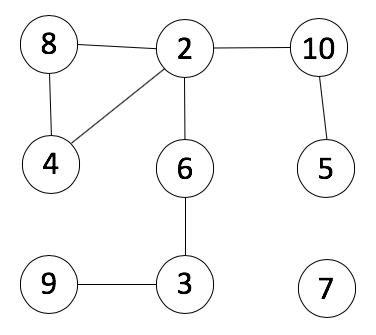
b) Here is one possible factor graph for the numbers 2 - 12.

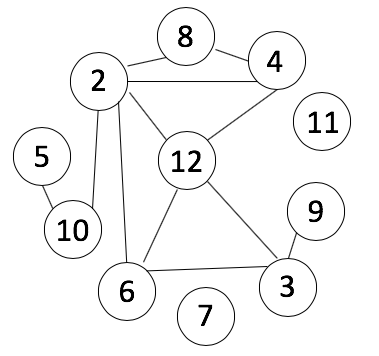
c) It is possible to make a factor graph for all the numbers from 2 - 23. Here is one way to do it.

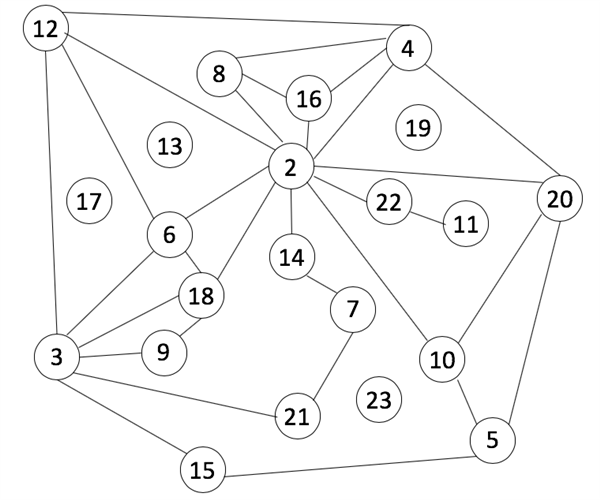
d) Because 1 is a factor of every number, if we included one, the graph would become impossible to draw (without crossing lines) much earlier!

a) 

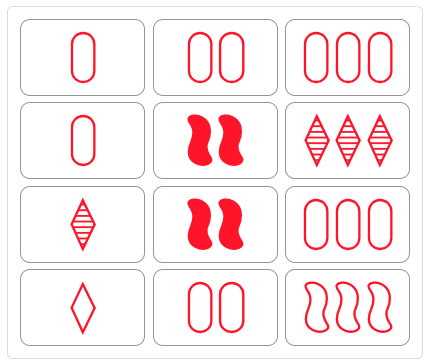
b)

c)