2019 - 2020

Archived Mathletes Problems of the Week   

 Solutions

 MPOW #1: Welcome Back Puzzlers

1. Amir wins by 4 games.
2. Josh drew 27 parallelograms.
3. The weight of one die, one ball, and one marble is 75 grams.

1. There are three possible trains of length 5.
2. There are five possible trains of length 6, eight possible trains of length 7, and thirteen possible trains of length 8.
3. The number of no-one trains follows the same pattern as the Fibonacci Sequence. Therefore, the number possible trains of length 12 is the 12^th Fibonacci number: 89. (Note: because there are no possible 1 trains, the first Fibonacci number in this sequence is 0).

1. There are 9 two-digit palindromic numbers. They are all of the multiples of 11 where both digits are the same.
2. There are 90 three-digit palindromic numbers. They look like these numbers 101, 111, 121, 131, 141, … 545, 555, 565, 575, … 979, 989, 999.
3. This procedure will work for almost every number. Most numbers will end up as a palindrome within five or six steps, like 68. A few numbers have been found that do not seem to ever create a palindrome, like 196.

1. Pierce mathematicians used a variety of recording methods to show all the steps in their solutions. You can see some of them on the bulletin board.
2. Here is John Urschel’s solution, which is the shortest possible and takes 15 steps.

a) Figures 5, 6, and 7 look like this. They contain 12, 15, and 18 dimes respectively.

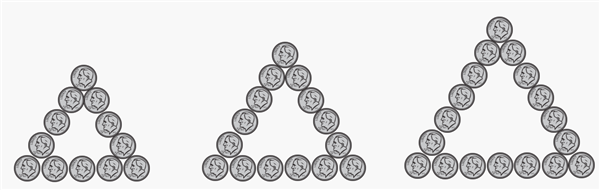
b)

figure - value in dimes - value in quarters

1       -      $0.10         -      $0.25

2       -      $0.30         -      $0.75

3       -      $0.60         -      $1.50

4       -      $0.90         -      $2.25

5       -      $1.20         -      $3.00

6       -      $1.50         -      $3.75

7       -      $1.80         -      $4.50

c) Figure 100 will have one side with 100 dimes. The second side will have 99 dimes, because one will be shared with the first side at the vertex of the triangle. The third side will have 98 dimes, because one will be shared with each of the other two sides at the vertices. It will have a total of 297 dimes and be worth $29.70.

d) When we fill in the inner part of the triangle, figures 5, 6 and 7 will look like this. Now, they contain 15, 21, and 28 dimes respectively.

figure - value in dimes - value in quarters

1       -      $0.10         -      $0.25

2       -      $0.30         -      $0.75

3       -      $0.60         -      $1.50

4       -      $1.00         -      $2.50

5       -      $1.50         -      $3.75

6       -      $2.10         -      $5.25

7       -      $2.80         -      $7.00

Figure 100 will have a row of 100 dimes on the bottom, then the next row will have 99, the next row 98, and so on until the top row that has 1 dime. It will have a total of 5050 dimes and be worth $505.00.

a) The team could have scored 2 glomstars and 10 slurfs. There are no other ways to make the score 82.

b) Some other impossible scores include: 1, 2, 3, 4, 5, 7, 8, 9, 10, 13, 14, 15, 16… There are a total of 25 impossible scores. The highest impossible score is 49.

c) If teams can score 2 points for a pwelly, then all scores after 9 become possible.

1. In order to have a Friday the 13^th, the month has to start on a Sunday.
2. The only two consecutive months that can both have a Friday the 13^th are February and March.
3. Every year will have at least one Friday the 13^th, but no year can have more than three Friday the 13^ths.
4. At the end of 2019, we will have had 35 Friday the 13^ths in the 2000s.

a) Here is the price of each letter:

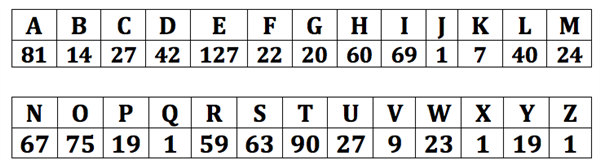
b) Answers will vary.

a) There are 10 ways to make 4-in-a-row on a grid with 4 rows and 4 columns.

b) On a grid with 4 rows and 5 columns, there are 17 ways to make 4-in-a-row.

c)  On a grid with 4 rows and 6 columns, there are 24 ways to make 4-in-a-row, and on a grid with 4 rows and 7 columns, there are 31 ways to make 4-in-a-row. Each time we add another column, there are 7 more ways to make 4-in-a-row. We get one more way straight down that column, one more way in each row, and two more diagonal ways.

d) On a grid with 5 rows and 5 columns, there are 28 ways to make 4-in-a-row. Each time we add a column to the 5-row board, we gain 11 new ways to make 4-in-a-row: 2 in the new column, 1 in each of the original 5 rows, and 4 new diagonals.

e) The standard board has 6 rows and 7 columns. There is a similar pattern as boards of this size grow. We can start with a smaller 6 row-4 column board and see there are 24 possible winning lines. When we add a new column we gain 15 new winning lines. So the standard 6 row-7 column board has 69 winning lines.

a) There are a total of 6 three-digit numbers that have a digit product that is equal to 4.

b) There are a total of 10 three-digit numbers that have a digit product that is equal to 8.

c)  There are a total of 15 three-digit numbers that have a digit product that is equal to 12.

d) It is impossible to make three-digit numbers that have a digit product equal to a two-digit prime number such as 11 or 13 or any multiple of a two-digit prime.

e) The digit product between 1 and 25 that can be made the most number of ways is 24. There are twenty-one three-digit numbers with a digit product of 24.

a) If Anne has one friend, Bob has two friends, Carl has three friends and Elisa is friends with everyone, then Diana has two friends.

If Anne has one friend, Bob and Carl each have two friends and Elisa is friends with everyone, then Diana either has one friend (if Bob and Carl are friends with each other) or three friends (if Bob and Carl are not friends with each other.)

b)

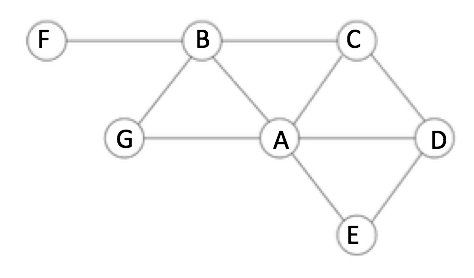
a) The tetrahedron has 4 vertices, 6 edges, and 4 faces. The cube has 8 vertices, 12 edges, and 6 faces. The octahedron has 6 vertices, 12 edges, and 8 faces. The dodecahedron has 20 vertices, 30 edges, and 12 faces. The icosahedron has 12 vertices, 30 edges, and 20 faces. Euler noticed that, for these particular 3D solids (ones where all the faces are identical regular polygons), if you add the number of vertices and faces, the sum will always be two more than the number of edges.

b) The minimum number of colors required to color the tetrahedron is 4. The cube requires 3 colors. The octahedron requires 2. The dodecahedron needs 4 colors. And the icosahedron requires 3.

a) To go back to your 12^th birthday, you could use:

    - C four times (8 steps)

    - A three times (21 steps)

b) To go back to your 11^th birthday, you could use:

      - C eight times (16 steps)

      - B three times and C once (17 steps)

      - A once, B twice, and C twice (21 steps)

      - A twice, B once, and C three times (25 steps)

      - A three times and C four times (29 steps)

      - A six times (42 steps)

c) If you took a total of 24 steps, you could have used and travelled:

      - A twice and B twice, travelling 22 months back

      - A once, B three times, and C once, travelling 28 months back

      - A once, B once, and C six times, travelling 29 months back

      - B four times and C twice, travelling 34 months back

      - C twelve times, travelling 36 months back

d) If you travelled back to your 8^th birthday using 25 backward steps, you could have used and taken:

      - A once and C seven times, taking 21 forward steps

      - A four times and C three times, taking 34 forward steps

Some numbers that fit in each region are listed below. Unless stated otherwise, other numbers may also be possible.

a) 

Section A: 31, 36, 38, 5271…

Section B: 5, 4, 3, 1, -15…

Section C: Impossible. There are no numbers that are both less than 6 and greater than 30.

Section D: 7 through 29, but not 12 or 22

Section E: 2, -2, -12…

Section F: 32, 42, 7002...

Section G: 12 and 22 only

Section H: Impossible. There are no numbers that are both less than 6 and greater than 30.

b)

Section A: 15, 30, 750…

Section B: 1 and 2 only

Section C: 12, 24, 404…

Section D: 5, 10 only

Section E: 4, 8 only

Section F: 60, 100, 1020...

Section G: 20 and 40 only

Section H: 3, 6, 7, 9, 42…

c)

Section A: 3/4, 7/6, 1…

Section B: 0/10, 1/4, 49/99…

Section C: Impossible. There are no numbers that are both less than 1/2 and larger than 2/3.

Section D: 5/7, 7/12, 6/10…

Section E: 1/2, 2/7, 10/41…

Section F: 4/3, 6/7, 71/101…

Section G: 3/5, 5/7, 6/11…

Section H: Impossible. There are no numbers that are both less than 1/2 and larger than 2/3.

a. Each section is half as large as the previous section. The denominators are increasing powers of 2. Any section n will be 1/2ⁿ in size. See the table below for details. 

b. The area of each section is half the size of the previous section. Any section n will have an area of 100 ÷ 2ⁿ. See the table below for details. 

c. At each stage, we still have one fractional part missing. The sum of all sections up to any section n will be (2ⁿ – 1)/ 2ⁿ. See the table below for details. 

d. After we add in the 7^th section, we will have over 99% of the area of the original shape.

Square Pattern

e. The new shape is similar, but a little more complicated to write an expression for. The size of the pieces becomes 4 times smaller every three pieces. We can find the proper power of 4 for any section by using a floor function. The fraction that section n will be is 1/4^f, where f is the expression (n + 2)/3, rounded down to the nearest whole number. See the table below for details. 

Triangle Pattern

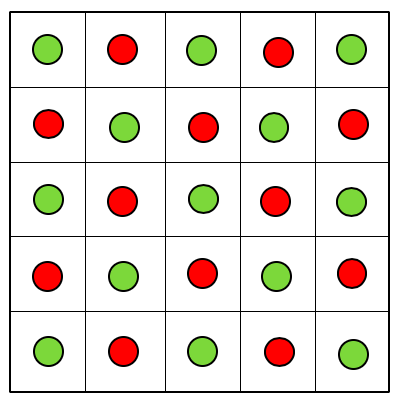
Rooms you can escape from are shown in green. Rooms you cannot escape from are shown in red.

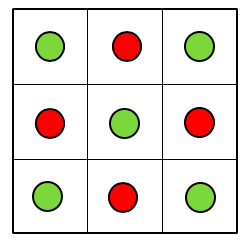
a. In a 3 x 3 house, you can travel through every room exactly once and escape only if you start from the room in the center or from one of the rooms in the four corners. If you start in one of the other four rooms, it is impossible to travel through every room once and escape.

b. In a 4 x 4 house, you can travel through every room exactly once and escape from any room.

c. In a 5 x 5 house, the rooms you can escape from are shown above. 

Notice that the 5 x 5 house is just a larger version of the 3 x 3 house. We can predict that any odd number square house will have a similar pattern. Similarly, the a 6 x 6 house will be just a larger version of the 4 x 4 house, so we can predict that in an even number square house, we can escape from any room.

d. We can make a loop from any room in the 4 x 4 house. We cannot make a loop from any of the rooms in the 3 x 3 house or the 5 x 5 house. 

a.

1! = 1

2! = 1 x 2 = 2

3! = 1 x 2 x 3 = 6

4! = 1 x 2 x 3 x 4 = 24

5! = 1 x 2 x 3 x 4 x 5 = 120

6! = 1 x 2 x 3 x 4 x 5 x 6 = 720

7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 5,040

8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40,320

9! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 = 362,880

10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 3,628,800

b.  The largest power of 2 that is a factor of 10! is 2⁸. The largest powers of the other numbers that are factors of 10! are as follows: 3⁴, 4⁴, 5², 6⁴, 7¹, 8², 9², and 10².

c. n must be 16.

d. Six weeks is equal to 3,628,800 seconds, which is 10! seconds.

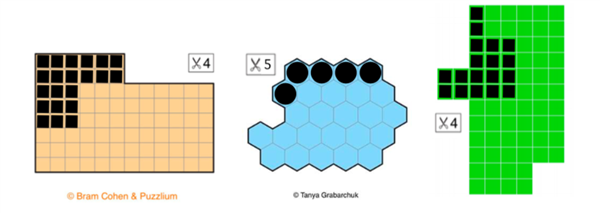
In each shape, one of the identical pieces is highlighted in black.

a) All odd numbers, starting with 3, can be written as 2-row trapezoidal numbers. We can use the expression 2n + 1 to describe these numbers.

b) All the multiples of three, starting with 6, can be written as 3-row trapezoidal numbers. We can use the expression 3n + 3 (or an equivalent expression) to describe these numbers.

c) The 4-row trapezoidal numbers begin 10, 14, 18, 22… and are spaced four apart. One expression for these numbers is 4n + 6. The 5-row trapezoidal numbers begin 15, 20, 25, 30… and continue with all the multiples of five. One expression for these is 5n + 10. The 6-row trapezoidal numbers begin 21, 27, 33, 39… and are spaced 6 apart. One expression for these is 6n + 15. We can see a pattern in these expressions that would allow us to create a general expression for any r-row trapezoidal number: r x n + (r - 1)^th triangle number.

d) Yes, 100 can be written as a 5-row trapezoidal number: 18 + 19 + 20 + 21 + 22. It can also be written as a 8-row trapezoidal number: 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16.

e) The numbers that cannot be written as trapezoidal numbers are the powers of 2: 1, 2, 4, 8, 16, 32…. This is because they do not have any odd factors.

a. There are 12 ways to spell WHO.

b. There are 30 ways to spell MAFFY.

c. There are 64 paths that spell ROTOR.

d. There are 84 paths that spell BANANA.

a. Here are the steps to fold the “Level 1” paper to stack the numbers on top of each other in order.

• Fold the paper in half so that the 1 goes over the 4. You should now see the 8 and 1 at the top.
• Fold the paper in half so that the 2 goes behind the 1. You should see 8 and 1 on the front and 2 and 3 on the back.
• The 4 and 5 are inside between the 1 and 2. Hold those two together and tuck them between the 3 and 6.
• Fold the 1 behind the 8. You should see the 8 on front and the 1 on the back.
• Flip over and the numbers should be in order.

b. Here are the steps to fold the “Level 2” paper to stack the numbers on top of each other in order.

• Fold the paper in half so that the bottom row of numbers goes behind the top row of numbers. You should now see the 1, 8, 2, 7 row.
• Fold the 1 behind the 8. You should now see 8, 2, 7.
• Open up the paper between the 1 and the 4. Hold the 7 and the 6 together and slide them between the 1 and 4. Continue that sliding, so that the 7/6 ends up between the 8/5 and the 2/3 ends up between the 1/4.
• Flip over and the numbers should now be in order.

a. The other four-digit autobiographical number is 2020.

b. The only five-digit autobiographical number is 21200.

c. There are no one-digit, two-digit, or three-digit autobiographical numbers.

d. The only ten-digit autobiographical number is 6210001000.

e. The digit sum of every autobiographical number is equal to the total number of digits the number has. This is because each place value in the number is essentially a tally of how many of that digit there are. In a ten-digit number, for example, there have to be exactly ten digits, so the tallies will add up to ten.

a.

b.

c.

d.

e.

a. The 2 by 2 knot has two loops; the 4 by 4 knot has four loops; the 5 by 5 knot has five loops; and the 6 by 6 knot has six loops.

b. Square loops like these have the same number of loops as their side dimension.

c. Each of these rectangular knots has one loop.

d. The 6 by 8 knot has two loops; the 6 by 9 knot has three loops; and the 7 by 14 knot has two loops.

e. The number of loops in a rectangular knot is determined by the greatest common factor of the two side dimensions. (Note: this is also true of the square knots.)

f. 

 .